حل دستگاه معادلات غیر خطی با الگوریتم ژنتیک در پایتون
الگوریتم های تکاملی و فراابتکاری در سال های اخیر با توجه به عملکرد خوبی که از خود نشان داده اند توجه زیادی از پژوهشگران را به خود جلب نموده است و تاکنون برای حل مسائل مختلفی از جمله مسائلی که np-hard هستندمورد استفاده قرار گرفته اند. حل مسائل np-hard توسط الگوریتم های بهینه سازی دقیق برای ابعاد بالا به زمان خیلی بیشتر نیاز دارند یا غیر ممکن هستند. به عنوان مثال اگر مسئله فروشنده دوره گرد(TSP) تعداد شهرها زیاد شود بدین ترتیب بعد مسئاله افزایش میابد و فضای جستجو و حالت های ممکن جواب بصورت نمایی افزایش می یابد که در این شرایط حل کردن آن با الگوریتم های بهینه سازی دقیق بسیار سخت خواهد بود و به رمان بیشتری نیاز خواهد داشت.
بنابراین الگوریتم های فراابتکاری با تولید جواب های اولیه تصادفی به تعداد جمعیت اولیه، و بروزرسانی آنها توسط عملگرهای خود سعی در پیدا کردن یک جواب بهینه سراسری هستند طوری که تابع هدف کمینه(بیشینه) شود. الگوریتم های فراابتکاری همه حالات ممکن جواب ها را بررسی نمیکنند و بدین طریق برای مسائل np-hard بهتر هستند.
الگوریتم ژنتیک یکی از مشهورترین و محبوب ترین الگوریتم های تکاملی هستند که تاکنون در مسائل زیادی بکار گرفته شده است و عملکرد بهتری را هم از خود نشان داده است.
مراحل اصلی الگوریتم ژنتیک بصورت زیر است:
۱-تولید جواب های اولیه به تعداد جمعیت بطور تصادفی از فضای جستجو(فضای جواب)
۲-محاسبه مقدار تابع هدف برای این جواب ها و یافتن بهترین جواب(در مساله مینیم سازی، بهترین جواب کمترین مقدار تابع هدف را دارد)
۳-انتخاب جواب های والد براساس میزان برازندگی آن ها توسط یک رویکرد انتخاب مانند روش چرخ رولت.(میزان برازندگی جواب ها با مقدا تابع هدف آن ها رابطه مستقیم دارد به عنوان مثال جوابی که مقدار تابع هدف آن در یک مسئله کمینه سازی از همه کمتر است احتمال انتخاب شدن آن به عنوان والد از بقیه جواب ها بیشتر است.)
۴-پس از اینکه درصدی از جمعیت به عنوان والد انتخاب شدند آن ها توسط عملگرهای برش(crossover) و جهش(mutation) با هم ترکیب شده و جواب های فرزند را تولید می نمایند.
۵- جواب های فرزند به سایر جواب های موجود در جمعیت افزوده شده و پس از اینکه مقدار تابع هدف آن ها محاسبه شد براساس برازندگی(fitness)، جمعیت حاضر مرتب می شوند و به تعداد جمعیت اولیه(npop) از بین آن ها به نسل بعد راه میابند و افراد ضعیف جمعیت از بین می روند.
۶- الگوریتم به مرحله ۲ می رود و این فرایند تا ماکزیمم تکرار (max_itr) تکرار می گردد و الگوریتم به پایان می رسد و نهاینا بهترین جواب حاصل به عنوان جواب بهینه سراسری برگردانده می شود.
ما در این پست معادلات غیر خطی را توسط الگوریتم ژنتیک(Genetic Algorithm) با زبان پایتون(python) حل نموده ایم.
معادله ای که حل کردیم بصورت زیر است که برای الفا، بتا و تتا های مختلف کد پایتون نوشته شده می تواند این معادله را حل نماید:
تابع هدف استفاده شده در این الگوریتم بصورت زیر تعریف شده است و به عنوان یک مسئله مینیم سازی در نظر گرفته شده است:
که در آن Squared Error باید مینیم گردد تا بهترین جواب حاصل شود.
کد پایتون الگوریتم ژنتیک برای حل دستگاه معادله را می توانید در ادامه دانلود نمایید.
Genetic Python Codes for nonlinear equations
قیمت: ۵۰۰۰۰۰ تومان
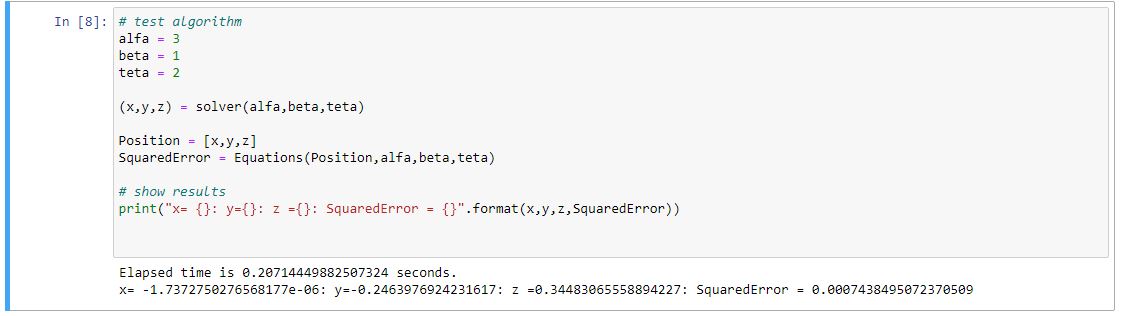
خروجی یک اجرا از این الگوریتم بصورت زیر است: